Convex functions

Consider the optimization problem 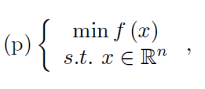........................\((10)\)

where \(f\) is a convex function and \(A∈\mathbb{R}^{m×n}\). A point \(x∈\mathbb{R}^{n}\) is optimal to \((10)\) if and only if it is feasible and \(∃μ∈\mathbb{R}^{m} s.t.∇f(x)=A^{T}μ.\)

Since this is a convex problem, our optimality condition tells us that feasible \(x\) is optimal if \(∇f^{T}(x)(y-x)≥0,∀y \; s.t.\; Ay=b\)

Any y with \(Ay=b\) can be written as \(y=x+v\), where \(v\) is a point in the nullspace of \(A\); i.e., \(Av=0\). Therefore, a feasible \(x\) is optimal if and only if \(∇f^{T}(x)v≥0,∀v \; s.t.\; Av=0.\) For any \(v\), since \(Av=0\) implies \(A(-v)=0\), we see that \(∇f^{T}(x)v≤0.\) Hence the optimality condition reads \(∇f^{T}(x)v=0,∀v \; s.t.\; Av=0.\)

This means that \(∇f(x)\) is in the orthogonal complement of the nullspace of \(A\) which we know from linear algebra equals the row space of \(A\) (or equivalently the column space of \(A^{T}). \text{ Hence }∃μ∈\mathbb{R}^{n} \; s.t.\; ∇f(x)=A^{T}μ.\)