Theorem
Theorem
Consider an optimization problem 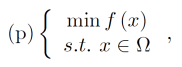
where \(f:\mathbb{R}^{n}\rightarrow \mathbb{R}\) is convex and differentiable and \(Ω\) is convex. Then a point \(x\) is optimal if and only if \(x∈Ω\) and \(∇f(x)^{T}(y-x)≥0,∀y∈Ω.\)
Consider an optimization problem 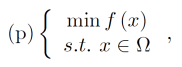
where \(f:\mathbb{R}^{n}\rightarrow \mathbb{R}\) is convex and differentiable and \(Ω\) is convex. Then a point \(x\) is optimal if and only if \(x∈Ω\) and \(∇f(x)^{T}(y-x)≥0,∀y∈Ω.\)