Remarks and explanation
What does this condition mean?
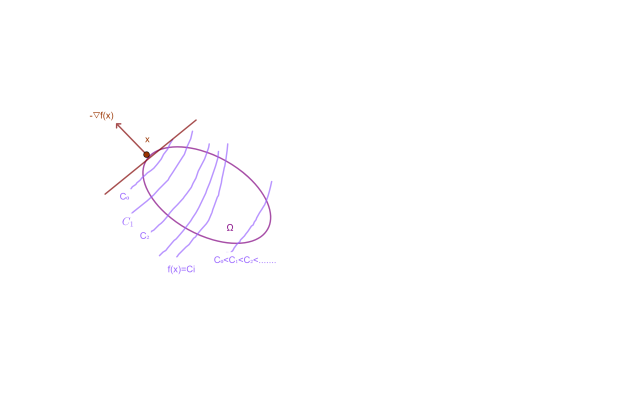
If you move from \(x\) towards any feasible \(y\), you will increase f locally.
The vector \(-∇f(x)\) (assuming it is nonzero) serves as a hyperplane that "supports" the feasible set \(Ω\) at \(x\). (See figure below) An illustration of the optimality condition for convex optimization.
Remark 1
The necessity of the condition holds independent of convexity of \(f\). Convexity is used in establishing sufficiency.
Remark 2
If \(Ω=\mathbb{R}^{n}\), the condition above reduces to our first order unconstrained optimality condition \(∇f(x)=0.\)
Remark 3
Similarly, if \(x\) is in the interior of \(Ω\) and is optimal, we must have \(∇f(x)=0\). (Take \(y=x-α∇f(x)\) for \(α\) small enough.)