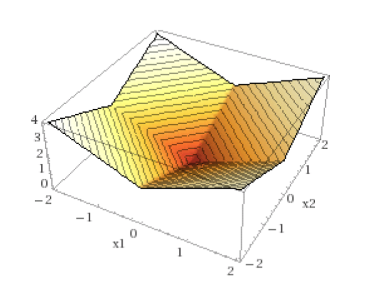
Examples of multivariate convex functions
Example : Affine functions:
The functions \(f(x)=a^{T}x+b\) with \(a∈\mathbb{R}^{n},b∈\mathbb{R}\) ) are convex, but not strictly convex; they are also concave:
\(∀λ∈[0,1],f(λx+(1-λ)y) = a^{T}(λx+(1-λ)y)+b\)
\(\hspace{5,7cm}= λa^{T}x+(1-λ)a^{T}y+λb+(1-λ)b\)
\(\hspace{5,7cm}= λf(x)+(1-λ)f(y).\)
In fact, affine functions are the only functions that are both convex and concave.
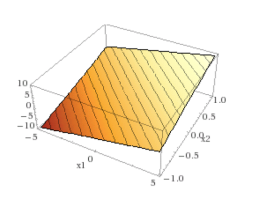
Example : Some quadratic functions:
Let \(f(x)=x^{T}Qx+c^{T}x+d,\) where \(Q\) is a matrix of order \(n\times n,\) \(c\in\mathbb{R^n}\) and \(d\in \mathbb{R}\). We have
\(f\) is Convex if and only if \(Q≥0\).
\(f\) is Strictly convex if and only if \(Q>0\).
\(f\) is Concave if and only if \(Q≤0\); strictly concave if and only if \(Q<0\).
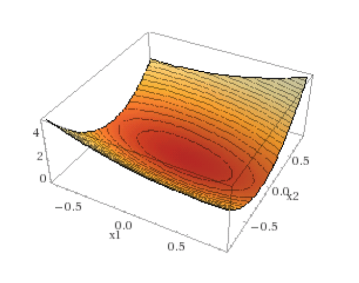
Example : Any norm
Recall that a norm is any function f that satisfies:
\(f(αx)=|α|f(x),∀α∈\mathbb{R}.\)
\(f(x+y)≤f(x)+f(y).\)
\(f(x)≥0,∀x,f(x)=0⇒x=0.\)
So
\(\hspace{3cm}∀λ∈[0,1],f(λx-(1-λ)y)≤f(λx)+f((1-λ)y)=λf(x)+(1-λ)f(y)\),
where the inequality follows from triangle inequality and the equality follows from the homogeneity property.