Definitions and examples
Definition :
A function \(f:\mathbb{R}^{n}\rightarrow \mathbb{R}\) is convex if its domain is a convex set and for all \(x,y\) in its domain, and all \(λ\)∈[0,1], we have
\(\hspace{5cm}\)\(f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y)\)
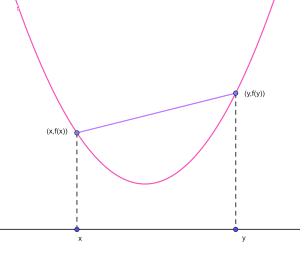
Geometrically, the line segment connecting \((x,f(x))\) to \((y,f(y))\) must site above the graph of \(f\).
Remarks
In words, this means that if we take any two points \(x,y\), then f evaluated at any convex combination of these two points should be no larger than the same convex combination of \(f(x)\) and \(f(y)\).
If \(f\) is continuous, then to ensure convexity it is enough to check the definition with \(λ\)=\(\frac{1}{2}\) \(\hspace{5cm}\) (or any other fixed \(λ\)∈(0,1)).
Definition :
We say that \(f\) is concave if \(-f\) is convex.
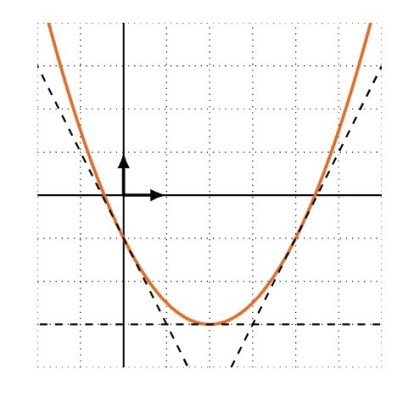
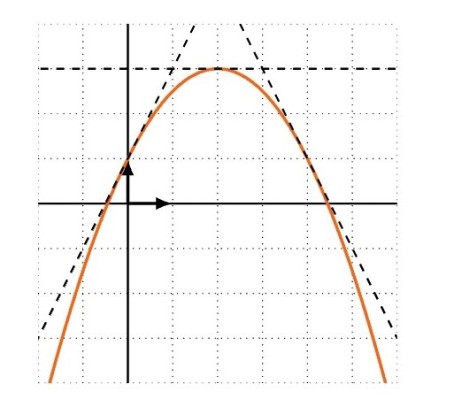
Example :
The functions \(f(x)=x^{2}\) is convex on \(\mathbb{R}^{n}\) . Let \(a\in\mathbb{R}\) , the equation of the tangent in \(a\) is \(y=f′(a)(x-a)+f(a)\).
So,
\(\hspace{5cm} y=2ax-2a^{2}+a^{2}=2ax-a^{2}\).
Then
\(\hspace{5cm}f(x)-(2ax-a^{2})=x^{2}-2ax+a^{2}=(x-a)^{2}≥0\)
which means that the tangent in \(a\) is above the graph of \(f\).
Example :
The function\( f(x)=x^{a}\) is convex on \( \mathbb{R}₊\), if \(a≥1\) or \(a≤0\)
and the function \(f(x)=log(x)\) is a concave function.