Quadratic functions revisited
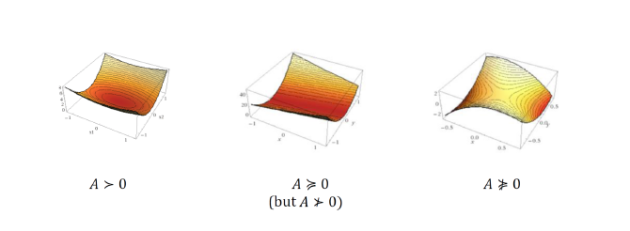
Let \(f(x)=x^{T}Ax+bx+c\) where \(A\) is symmetric. Then f is convex if and only if \(A≥0\), independently of \(b,c.\)
Consider now the unconstrained optimization problem :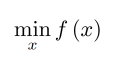 .......................\((7)\)
.......................\((7)\)
We can establish the following claims:
\(A≱0\) (\(f\) not convex)\(⇒\)problem \((7)\) is unbounded below.
Indeed, let \(x\) be an eigenvector with a negative eigenvalue \(λ\). Then
\(Ax=λx⇒x^{T}Ax=λx^{T}x<0\) and \(f(αx)=α^{2}x^{T}Ax+αbx+c\)
So \(f(αx)→-∞\) when \(α→∞.\)
\(A>0⇒f\) is strictly convex. There is a unique solution to\((7):\) \(x^{∗}=-(\frac{1}{2})A^{-1}b\)
\(A≥0⇒f\) is convex. If A is positive semidefinite but not positive definite, the problem can be unbounded (e.g., take \(A=0,b≠0\)), or it can be bounded below and have infinitely many solutions (e.g., \(f(x)=(x_{1}-x_{2})^{2}\)). One can distinguish between the two cases by testing whether b lies in the range of \(A\). Furthermore, it is impossible for the problem to have a unique solution if \(A\) has a zero eigenvalue.
Least square revisited
Recall the least square problem :![]()
Under the assumption that the columns of A are linearly independent,
\(x=(A^{T}A)^{-1}A^{T}b\) is the unique global solution because the objective function is strictly convex.