Convex functions

Consider an optimization problem

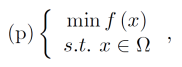
where \(f:\mathbb{R}^{n}\rightarrow \mathbb{R}\) is strictly convex on \(Ω\) and \(Ω\) is a convex set. Then the optimal solution (assuming it exists) must be unique.

Suppose there were two optimal solution \(x,y∈\mathbb{R}^{n}\). This means that \(x,y∈Ω\) and

\(\hspace{4cm}f(x)=f(y)≤f(z),∀z∈Ω.\)........................\((6)\)

Consider \(z=\frac{x+y}{2}\), by convexity of \(Ω\), we have \(z∈Ω\) and by strict convexity, we have

\(\hspace{3cm}f(z)=f(\frac{x+y}{2})<\frac{1}{2}f(x)+\frac{1}{2}f(y)=\frac{1}{2}f(x)+\frac{1}{2}f(x)=f(x).\)

But this contradicts \((6)\).