Corollary
Corollary
Consider an unconstrained optimization problem
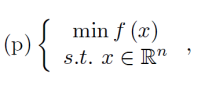
where \(f\) is convex and differentiable. Then, any point \(x\) that satisfies \(∇f(x)=0\) is a global minimum.
Proof
From the first order characterization of convexity, we have
\(\hspace{5cm}f(y)≥f(x)+∇f^{T}(x)(y-x),∀x,y.\)
In particular
\(\hspace{5cm}f(y)≥f(x)+∇f^{T}(x)(y-x),∀y\) for fixed \(x.\)
Since \(∇f(x)=0\), we get
\(\hspace{5cm}f(y)≥f(x),∀y.\)
Reminder :
Recall that \(∇f(x)=0\) is always a necessary condition for local optimality in an unconstrained problem. The theorem states that for convex problems, \(∇f(x)=0\) is not only necessary, but also sufficient for local and global optimality.
Remarks
In absence of convexity, \(∇f(x)=0\) is not sufficient even for local optimality ( e.g., think of \(f(x)=x^{3}\) and \(x=0\)).
Another necessary condition for (unconstrained) local optimality of a point \(x\) was \(∇^{2}f(x)≥0\). Note that a convex function automatically passes this test.