Principle Theorem
Theorem
Suppose \(f:\mathbb{R}^{n}\rightarrow \mathbb{R}\) is twice differentiable over an open domain. Then, the following properties are equivalent:
\(\hspace{1cm}(i)\) \(f\) is convex.
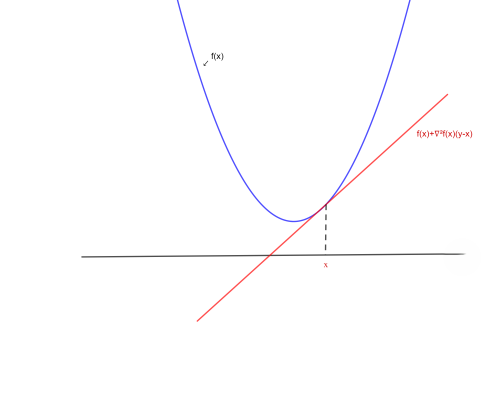
\(\hspace{1cm}(ii)\) \(f(y)≥f(x)+∇f^{T}(x)(y-x)\), for all \(x,y∈dom(f)\).
\(\hspace{1cm}(iii)\) \(∇^{2}f(x)≥0\), for all \(x∈dom(f)\).
Interpretation :
Condition \((ii)\): The first order Taylor expansion at any point is a global under estimator of the function.
Condition \((iii)\): The function \(f\) has nonnegative curvature everywhere. ( In one dimension\( f′′(x)≥0,∀x∈dom(f)\)).