Probabilités et statistiques

• On s'intéresse à la caractéristique $X$ d'une population ($X$=v.a.). On pose $E(x)=m,V(x)={\mathrm{\sigma }}^2$

• On note $(X_1,\cdots ,X_n)$l'échantillon aléatoire associé 1 à un sondage aléatoire simple de n individus de cette population $(x_1,\cdots ,x_n)$et une

  réalisation de celui ci (1 sondage particulier)

Empirique veut dire « de l'échantillon »

• Définition : $\overline{X_n}=\frac{1}{n}\sum _{i=1}^n{X}_i$

• Loi et moments : Loi inconnue en général

  $E(\overline{X_n})=m;V(\overline{X})=\frac{{\mathrm{\sigma }}^2}{n}$

• Propriétés asymptotiques

  • Loi des grands nombres

    $\overline{X_n}{\to }^{P}m;\overline{X_n}{\to }^{P\mathrm{.}S}m$

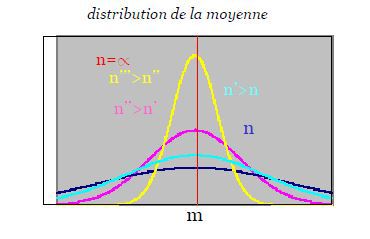
  • Théorème central limite (TCL)

    $\sqrt{n}\frac{\overline{X_n}-m}{\mathrm{\sigma }}{\mathrm{\to }}^{l}N(\mathrm{0,1})$

    $\sqrt{n}(\overline{X_n}-m){\mathrm{\to }}^{l}N(\mathrm{0,}\mathrm{\sigma })$

• $\overline{X_n}$ « approche» m : c'est un estimateur de m. Il est :

• - sans biais

• - asymptotiquement efficace

• - fortement convergent

• - la loi de l'erreur d'approximation est approximativement gaussienne lorsque n est grand

• Définitions :

  $S_n^2=\frac{1}{n}\sum _{i=1}^n{(X_i-\overline{X})}^2$

• Loi et Moments : La loi est généralement inconnue.

  $E(S_n^2)=\frac{n-1}{n}{\mathrm{\sigma }}^2,V(S_n^2)=\frac{n-1}{n^2}((n-1){\mathrm{\mu }}^4-(n-3){\mathrm{\sigma }}^4)$

• Lien entre $\overline{X_n}$ et$S_n^2$ ils sont asymptotiquement non corrélés :

  $\mathit{Cov}(\overline{X_n},S_n^2)=\frac{{\mathrm{\mu }}^3}{n}(1-\frac{1}{n})$

• Propriétés asymptotiques :

  $\sqrt{n}\frac{S_n^2-{\mathrm{\sigma }}^2}{\sqrt{{\mathrm{\mu }}^4-{\mathrm{\sigma }}^4}}{\mathrm{\to }}^{l}N(\mathrm{0,1})$

Si $X$ suit une loi$N(m,\mathrm{\sigma })$. Alors :

$\mathit{Cov}(S_n^{\mathrm{2,}}\overline{X_n^2})=0\mathrm{:}{S}_n^2\perp \overline{X_n}$

$\overline{X_n}\sim N(m,\frac{\mathrm{\sigma }}{\sqrt{n}})$

$\frac{{\mathit{nS}}_n^2}{{\mathrm{\sigma }}^2}\sim \mathrm{{\rm X}}(n-1)$